在用CSS写动画时需要设置动画的运动速度变化节奏，这个值是可以是根据四点定义一个 贝塞尔曲线。出于好奇了解一下贝塞尔曲线到底是啥。

贝塞尔曲线定义规则

简单概括，贝塞尔曲线是一组固定的点，起点向终点运动过程中，固定的点之间等比例关系点的集合。

在平面内任选 3 个不共线的点，依次用线段连接。

在第一条线段上任选一个点 D。计算该点到线段起点的距离 AD，与该线段总长 AB 的比例。

根据上一步得到的比例，从第二条线段上找出对应的点 E，使得 AD:AB = BE:BC。

连接这两点 DE。

从新的线段 DE 上再次找出相同比例的点 F，使得 DF:DE = AD:AB = BE:BC。

到这里，我们就确定了贝塞尔曲线上的一个点 F。

当D点由A向B点移动，而E点由B点向C点移动，根据等比例关系，可以绘制出一组F点的曲线。这条曲线就是贝塞尔曲线。

如果是4个点呢？

步骤都是相同的，只不过我们每确定一个贝塞尔曲线上的点，要进行三轮取点操作。如图，AE:AB = BF:BC = CG:CD = EH:EF = FI:FG = HJ:HI，其中点 J 就是最终得到的贝塞尔曲线上的一个点。

这样我们得到的是一条三次贝塞尔曲线

贝塞尔曲线公式

线性贝塞尔曲线：

二次方贝塞尔曲线：

三次方贝塞尔曲线：

P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P2之前，走向P1方向的“长度有多长”。

一般化

n阶贝塞尔曲线可如下推断。给定点P0、P1、…、Pn，其贝塞尔曲线

例如n=5：

原理推导（三阶）

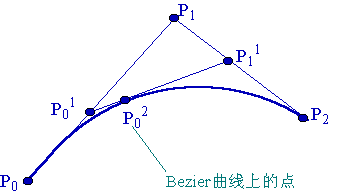
根据贝塞尔曲线定义的规则可知：

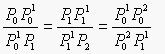
当P0，P2固定，引入参数t，令上述比值为t:(1-t)，即有：

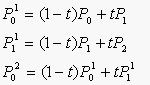
t从0变到1，第一、二式就分别表示控制二边形的第一、二条边，它们是两条一次Bezier曲线。将一、二式代入第三式得：

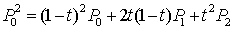
当t从0变到1时，它表示了由三顶点P0、P1、P2三点定义的一条二次Bezier曲线。

参考

贝塞尔曲线扫盲

贝塞尔曲线

贝塞尔曲线原理(简单阐述)