算法是计算机世界永恒的主题,现在世界其实是被算法驱动着进步.学习算法并能熟练在自己业务场景中应用各种算法应该是每个程序员必备的素质.从最基础的十大经典排序算法作为开始,开启自己系统学习算法之路!

冒泡排序(Bubble Sort)

思想

  • 冒泡排序只会操作相邻的两个元素
  • 每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求.如果不满足就让它们俩互换.
  • 冒泡排序算法最多进行 n-1次(n 排序数组长度),每次算法执行元素对比次数是n - i -1次(n 排序数组长度, i 当前算法循环次数)

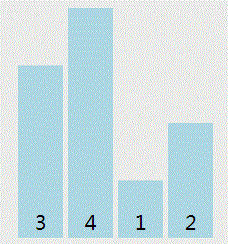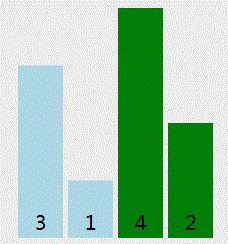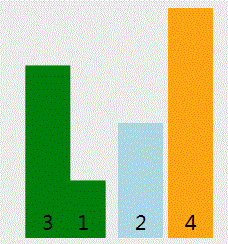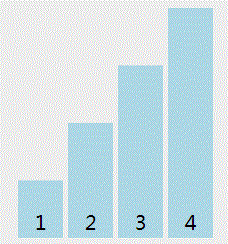
4208590040-5ac42b210af83_articlex.gif

116807884-57dcd3a8c4bf4_articlex.gif

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
const bubbleSort = (arr) => {
  const length = arr.length;
  if (length <= 1) return;
  // 冒泡排序算法最多执行次数是,排序数组长度 减 1.因为最后一次循环不需要执行.
  for(let i = 0; i < length -1; i++) {
    let hasChange = false; // 提前退出冒泡循环的标志
    // 冒泡排序中 元素比较次数是 当前是 排序数组长度 减 当前循环次数和1.因为 当前循环次数表示已经确定了位置的数字数量.
    for(let j = 0; j < length - i -1; j++) {
      if(arr[j] > arr[j+1]) {
        const temp = arr[j];
        arr[j] = arr[j+1];
        arr[j+1] = temp;
        hasChange = true;// 表示有数据交换
      }
    }
    if(!hasChange) break; // 如果 false 说明所有元素已经到位,没有数据交换,可以提前退出
  }
  console.log('arr :', arr)
}

const arr = [7, 8, 4, 5, 6, 3, 2, 1];
bubbleSort(arr);
// arr : [1, 2, 3, 4, 5, 6, 7, 8]

特点

优点:

  1. 排序算法基础,简单实用易于理解.

缺点:

  1. 比较次数多, 效率较低.

插入排序(Insertion Sort) - 直接插入排序

思想

直接插入排序的实现方式是:将未排序的数据,插入到有序序列中!插入的方式是,从后向前扫描有序序列,找到相应的位置插入.

  1. 从第一个元素开始,该元素被认为已排序的有序序列.
  2. 取出最后一个有序序列的下一个元素,在已排序的元素中从后向前扫描.
  3. 如果该元素(已排序)大于新元素(未排序),将该元素移到下一位置.
  4. 重复步骤3,直到找到已排序的元素小于或等于新元素的位置.
  5. 将新元素插入到第四步找到的位置.
  6. 重复步骤2 ~ 5.

插入排序

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
const insertionSort = arr => {
  const length = arr.length;
  if (length <= 0) return;
  let preIndex, current;
  for( let i = 1; i < length; i++) {
    preIndex = i - 1; // 参与比较 已排序元素的下标
    current = arr[i]; // 参与比较 未排序元素 当前
    while (preIndex >=0 && arr[preIndex] > current) {
      // 参与比较的 已排序元素 大于 未排序的元素时
      arr[preIndex + 1] = arr[preIndex]; //参与排序的已排序元素 需要向后移一位
      --preIndex; // 将下标向前移一位, 取一个新的 已排序的元素与 未排序的元素进行比较.
    }
    if (preIndex + 1 != i) {
      // 避免同一个元素赋值给自身
      arr[preIndex+1] = current; // 将 当前元素插入预留的空位
      console.log('arr:', arr)
    }
  }
  return arr;
}

// 测试
const array = [5, 4, 3, 2, 1];
console.log("原始 array :", array);
insertionSort(array);
// 原始 array:    [5, 4, 3, 2, 1]
// array:           [4, 5, 3, 2, 1]
// array:           [3, 4, 5, 2, 1]
// array:          [2, 3, 4, 5, 1]
// array:           [1, 2, 3, 4, 5]

插入排序 - 拆半插入(Binary Insertion Sort)

拆半插入排序是直接插入排序一种优化算法,它也属于插入排序.

思想

拆半插入排序和直接插入排序都是将未排序的元素和已排序的元素做比较,插入到合适的已排序队列中,它们不同点是,直接插入排序是从已排序队列尾部向前取已排列元素做比较.而拆半插入排序,是取已排序队列中间一个值做比较,然后再取上一部分或下一部分中间值做比较,直到找到正确的位置.

步骤:

  1. 取 0 ~ i-1的中间点(m=(i-1) >> 1), arr[i] 与 arr[m]进行比较,若 arr[i] < arr[m],则说明待插入的元素arr[i]应该处于数组0m索引之间;反之,则说明它应该处于数组mi-1索引之间.
  2. 重复步骤1.每次缩小一半的查找范围,直至找到插入的位置.
  3. 将数组中插入位置之后的元素全部后移一位.
  4. 在指定位置插入第i个元素.

注意: x>>1 是位运算中右移运算,表示右移一位,等同于 x除以2再取整,即 x>>1 == Math.floor(x/2).

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
const binaryInsertionSort = arr => {
  const len = arr.length;
  if (len <= 1) return;
  let current,i,j,low,high,m;
  for(i = 1; i< len; i++) {
    low = 0;
    high = i -1;
    current = arr[i];
    // 当 low大于 high时说明, low位置就是current需要插入位置
    while(low<=high) {
      // 步骤1&2: 拆半查找
      m = (low+high)>>1; // 注: x>>1 是位运算中的右移运算,表示右移一位,等同于 x除以2再取整,即 x>>1 === Math.floor(x/2)
      if( arr[i] >= arr[m]) {
        // 值相同时,切换到高半区,保证稳定性
        low = m+1; // 插入点在高半区
      } else {
        high = m-1;// 插入点在低半区
      }
    }
    for( j = i; j > low; j--) {
      // 步骤3: 插入位置之后的全部后移一位
       arr[j] = arr[j -1];
      console.log('array:', JSON.parse(JSON.stringify(arr)))
    }
    arr[low] = current; // 步骤4: 插入该元素
  }
  console.log('array:', JSON.parse(JSON.stringify(arr)))
  return arr;
}

const array = [5, 4, 3, 2, 1];
console.log('原始 array:', array);
binaryInsertionSort(array);
// 原始 array:  [5, 4, 3, 2, 1]
// array :     [5, 5, 3, 2, 1]
// array :     [4, 5, 5, 2, 1]
// array :     [4, 4, 5, 2, 1]
// array :     [3, 4, 5, 5, 1]
// array :     [3, 4, 4, 5, 1]
// array :     [3, 3, 4, 5, 1]
// array :     [2, 3, 4, 5, 5]
// array :     [2, 3, 4, 4, 5]
// array :     [2, 3, 3, 4, 5]
// array :     [2, 2, 3, 4, 5]
// array :     [1, 2, 3, 4, 5]

选择排序(Selection Sort)

思想

选择排序算法的实现思路和插入排序有些类似,将元素划分为已排序区间和未排序区间.选择排序每次从未排序区间中找到最小的元素,将其放到已排序区间的末尾.

步骤:

  1. 首先在未排序序列中找到最小(大)元素,存放在排序序列的起始位置.
  2. 再从剩余的未排序序列元素中寻找最小(大)元素,然后放到已排序序列的末尾.
  3. 重复第二步,直到所有元素排序完成.

选择排序

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
const selectionSort = arr => {
  const len = arr.length;
  let minIndex, temp;
  for(let i = 0; i < len -1; i++) {
    minIndex = i;
    for(let j = i+1; j < len; j++) {
      if(arr[j] < arr[minIndex]){
          // 寻找最小的数
      		minIndex = j; // 将最小数的索引保存
      }
    }
    temp = arr[i];
    arr[i] = arr[minIndex];
    arr[minIndex] = temp;
    console.log('array: ', arr);
  }
  return arr;
}

// 测试
const array = [5, 4, 3, 2, 1];
console.log('原始array:', array);
selectionSort(array);
// 原始 array:  [5, 4, 3, 2, 1]
// array:           [1, 4, 3, 2, 5]
// array:           [1, 2, 3, 4, 5]
// array:          [1, 2, 3, 4, 5]
// array:           [1, 2, 3, 4, 5]

归并排序(Merge Sort)

思想

归并排序是将一个数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了.

步骤,假设一个数组有N个元素:

  1. 将每对单个元素（默认情况下，已排序）归并为2个元素的有序数组
  2. 将2个元素的每对有序数组归并成4个元素的有序数组，重复这个过程……
  3. 最后一步：归并2个N / 2元素的排序数组（为了简化讨论，我们假设N是偶数）以获得完全排序的N个元素数组

归并排序采用分而治之（Divide and Conquer，缩写为D＆C）的思想，这是一个强大的解决问题的范例。
分而治之算法通过以下步骤解决（某种类型的）问题 - 比如我们的排序问题：划分步骤：将大的原始问题划分成较小的子问题并递归地解决较小的子问题，
解决步骤：结合较小的子问题的结果来产生较大的原始问题的结果。

归并排序动画

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
// mergeSort 用来分拆 数组
const mergeSort = arr => {
  // 采用自上而下的递归方法
  const len = arr.length;
  if (len < 2) return arr;
  // len >> 1 和Math.floor(len/2) 等价
  let middle = len >> 1;
  let left = arr.slice(0,middle); // 拆分为两个子数组
  let right = arr.slice(middle); // 拆分为两个子数组
  return merge(mergeSort(left), mergeSort(right));
}

const merge = (left,right) => {
  // 左右两个数组比较大小合并后的新数组
  const result = [];
  
  while(left.length && right.length) {
    // 比较左右两个数组大小,将小的插入 新数组中
    if(left[0] <= right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
    // 检查 左右两个数组是否还有数据
    while(left.length) result.push(left.shift());
    while(right.length) result.push(right.shift());
    
    return result;
  }
}

// 测试
const arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.time('归并排序耗时');
console.log('arr :', mergeSort(arr));
console.timeEnd('归并排序耗时');
// arr : [2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]
// 归并排序耗时: 0.739990234375ms

算法执行过程如👇图

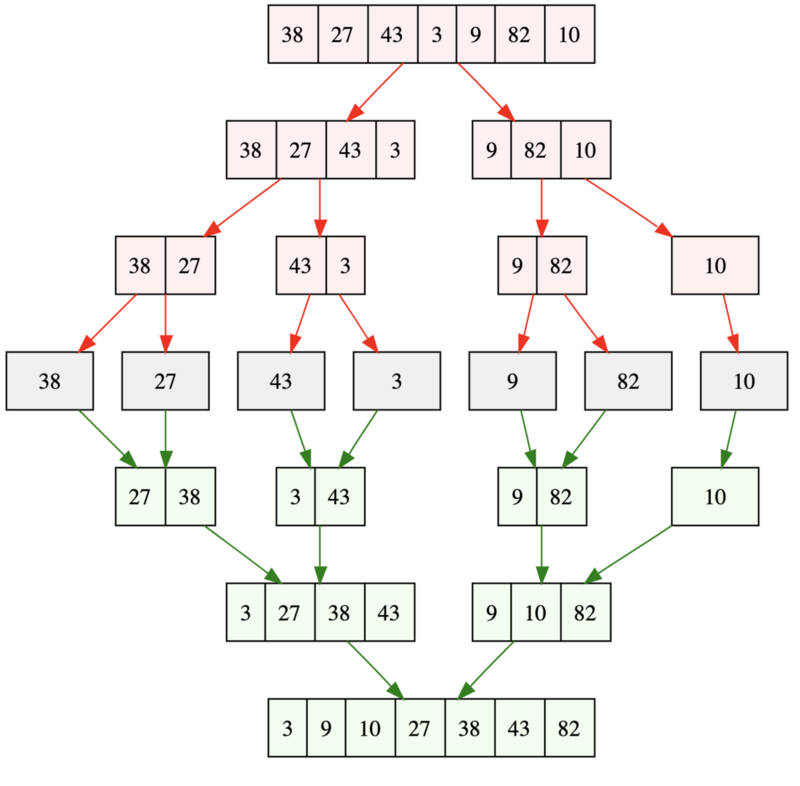
归并排序效果图

快速排序 (Quick Sort)

思想

快速排序通过在未排序队列中找一个基准点,通过和基准点比较,将比基准点大的元素放一个数组,比基准点小的元素放另一个数组.再在分类过一次的数组中找基准点重复上面的步骤,直至数组最后长度<=1.这时数组数据已经排序完成,只需要合并.

步骤:

  1. 先找到一个基准点(一般使用数组的中部或第一个元素),然后数组被该基准点分为两部分,依次与该基准点数据比较,如果比它小,放左边;反之,放右边.
  2. 左右分别用一个空数组去存储比较后的数据.
  3. 最后递归执行1、2操作,直到数组长度<=1;

快速排序是效率最高的排序算法之一,但它需要另外声明两个数组,需要使用内存资源更多.

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 方法一:
const quickSort1 = arr => {
  if (arr.length <= 1) return arr;
  // 取基准点
  const midIndex = len >> 1; // Math.floor(len / 2);
  // 取基准点的值, splice(index, 1) 则返回的是含有删除的元素数组.
  const midIndexVal = arr.splice(minIndex,1)[0];
  const left = []; // 存放比基准点小的数组
  const right = []; // 存放比基准点大的数组
  // 遍历数组, 进行判断分配
  for(let i = 0; i<arr.length; i++) {
    if(arr[i] < minIndexVal) {
      left.push(arr[i]); // 比基准点小的放左边数组
    } else {
      right.push(arr[i]); // 比基准点大的放右边数组
    }
    // 递归执行以上操作, 对左右两个数组进行操作,直到数组长度<=1;
    return quickSort1(left).concat(midIndexVal, quickSort1(right));
  }
}
const array2 = [5, 4, 3, 2, 1];
console.log('quickSort1 ', quickSort1(array2));
// quickSort1: [1, 2, 3, 4, 5]

上面👆的的实现方式是通过创建两个空数组left,right保存小于和大于基准点的值.

也有一种算法,不用创建空数组,直接通过操作原数组实现左右分离,逐步对比合并的操作.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// 快速排序
const quickSort = (arr, left, right) => {
  let len = arr.length,
    partitionIndex;
  left = typeof left != "number" ? 0 : left;
  right = typeof right != "number" ? len - 1 : right;

  if (left < right) {
    partitionIndex = partition(arr, left, right);
    console.log("arr", arr);
    quickSort(arr, left, partitionIndex - 1);
    quickSort(arr, partitionIndex + 1, right);
  }
  return arr;
};

const partition = (arr, left, right) => {
  //分区操作
  let pivot = left, //设定基准点的值（pivot）
    index = pivot + 1; // 分割点 我们将小于 基准点做放到 分割点的左边,而分割点右边都是大于基准点的值
  for (let i = index; i <= right; i++) {
    if (arr[i] < arr[pivot]) {
      swap(arr, i, index);
      index++; // 移动 分割点, 分割点的左边都是小于基准点的值
    }
  }
  swap(arr, pivot, index - 1); // 将 基准点放到分割点前一位
  return index - 1; // 返回基准点位置, 作为下次计算 数组的截至位置
};

const swap = (arr, i, j) => {
  let temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
};

let arr = [5, 1, 6, 3, 9, 4, 6, 2];
console.log('原数组:' arr);
console.log(quickSort(arr));
// 原数组: [ 5, 1, 6, 3, 9, 4, 6, 2 ]
// arr [ 2, 1, 3, 4, 5, 6, 6, 9 ]
// arr [ 1, 2, 3, 4, 5, 6, 6, 9 ]
// arr [ 1, 2, 3, 4, 5, 6, 6, 9 ]
// arr [ 1, 2, 3, 4, 5, 6, 6, 9 ]
// arr [ 1, 2, 3, 4, 5, 6, 6, 9 ]
// [ 1, 2, 3, 4, 5, 6, 6, 9 ]

上面算法实现的动图是这样的👇. 这样个算法消耗资源会更少,但理解起来会更困难(我是看了好久才明白)

快速排序

参考

https://segmentfault.com/a/1190000019916376

https://visualgo.net/zh/sorting?slide=1